AtCoder Beginner Contest 407 题解

AtCoder Beginner Contest 407

A-Approximation

题意：

给定一个正整数 $A$ 和一个正的奇整数 $B$，求一个整数，使它与 $\frac{A}{B}$ 的差最小。可以证明，在题目约束下，这样的整数是唯一的。

数据范围

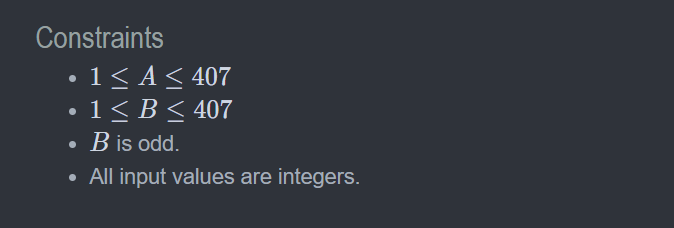
输入

题解：

对于给定的数据范围直接暴力枚举每一个即可

n,odd=RR()
a,b=int(n/odd),ceil(n/odd)
if abs(n/odd-a)<abs(n/odd-b):
    print(a)
else:
    print(b)

B - P(X or Y)

题意：

投掷两个六面骰子（点数分别是 1 到 6），求这两个点数的组合中，有多少种满足如下两个条件之一的情形，并计算其概率：

• 两个点数之和 不小于 $X$；
• 两个点数之差的绝对值 不小于 $Y$。
  两个骰子相互独立，且每个面出现的概率相等。

数据范围：

输入

题解：

同样，对于给定的数据范围直接看枚举即可

total=ans=0
x,y=RR()
for i in range(1,7):
    for j in range(1,7):
        total+=1
        if abs(i-j)>=y or i+j>=x:
            ans+=1
print(ans/total)

C - Security 2

题意：

在 AtCoder 公司门口有一个密码输入装置，包含一个屏幕和两个按钮。屏幕上显示一个字符串 $t$，初始为空串。按钮的功能如下：

• 按下按钮 A：在当前字符串末尾添加一个 0；
• 按下按钮 B：将字符串中的每一位数字都加 1（9 变为 0，即按模 10 循环）。

给定目标字符串 $S$，从空字符串开始，通过若干次按键，使得屏幕显示的字符串变为 $S$。请计算所需的最少按键次数。

数据范围：

输入

题解：

直接模拟做不要多想，从后往前考虑，最后一个位置一定要操作nums[-1]次，在操作的过程中前面的位置也一定会出现被连带着操作，因此累加操作次数cur，然后继续向前遍历即可。

s=RS()
n=len(s)
cur=ans=0

for i in range(n-1,-1,-1):
    c=int(s[i])
    c=(c-cur)%10
    ans+=c+1 # 加一是因为在末尾添加一个0
    cur+=c
print(ans)

D - Domino Covering XOR

题意：

给定一个 $H \times W$ 的网格，每个格子 $(i, j)$ 上有一个非负整数 $A_{i,j}$。你可以在网格上放置若干个多米诺骨牌，每个骨牌覆盖两个相邻的格子（只能是左右相邻或上下相邻），且每个格子至多被一个骨牌覆盖。

定义得分为没有被任何骨牌覆盖的格子中的所有整数的按位异或值（XOR）。

求最大可能得分。

数据范围：

输入

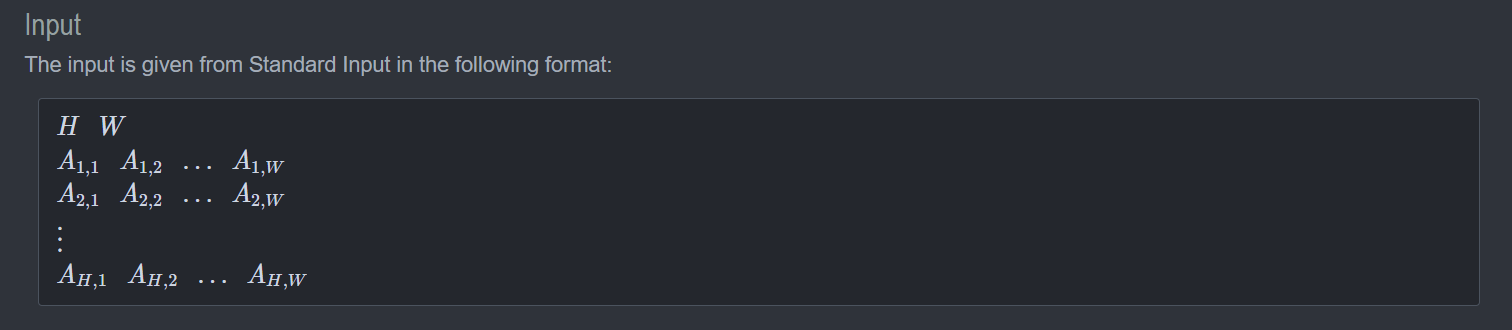
题解：

一开始这个数据范围没多想就直接上状压DP了，后来样例过不了才反应过来异或值怎么能返回最大

本题应当使用DFS，直接暴力搜索每个位置是否放骨牌，直接暴力也不行要把每个位置是否选过的状态压缩，不能用集合

m,n=RR()
g=[]
for _ in range(m):
    g.extend(RR())

ans=0
def dfs(pos,s):
    global ans
    if pos==n*m:
        res=0
        for i in range(n*m):
            if (s>>i)&1==0:
                res^=g[i]
        ans=max(ans,res)
        return  
    if (s>>pos)&1:
        dfs(pos+1,s)
        return 
    dfs(pos+1,s)
    x,y=divmod(pos,n)
    for dx,dy in (1,0),(0,1):
        if 0<=(i:=dx+x)<m and 0<=(j:=dy+y)<n:
            nx=i*n+j
            if s>>nx&1==0:
                dfs(pos+1,s|(1<<nx)|(1<<pos))

dfs(0,0)
print(ans)

E - Most Valuable Parentheses

题意：

给定一个长度为 $2N$ 的非负整数序列 $A = (A_1, A_2, \dots, A_{2N})$。

定义括号序列 $s$ 的得分方式如下：

• 对于 $s$ 中每一个为右括号 ) 的位置 $i$，将 $A_i$ 设为 0，最后对所有 $A$ 中的数求和，得到得分。

现在请你找出一个合法的括号序列 $s$（即左右括号配对匹配）使得这个得分最大。

一共 $T$ 个测试用例，分别求解。

数据范围：

输入

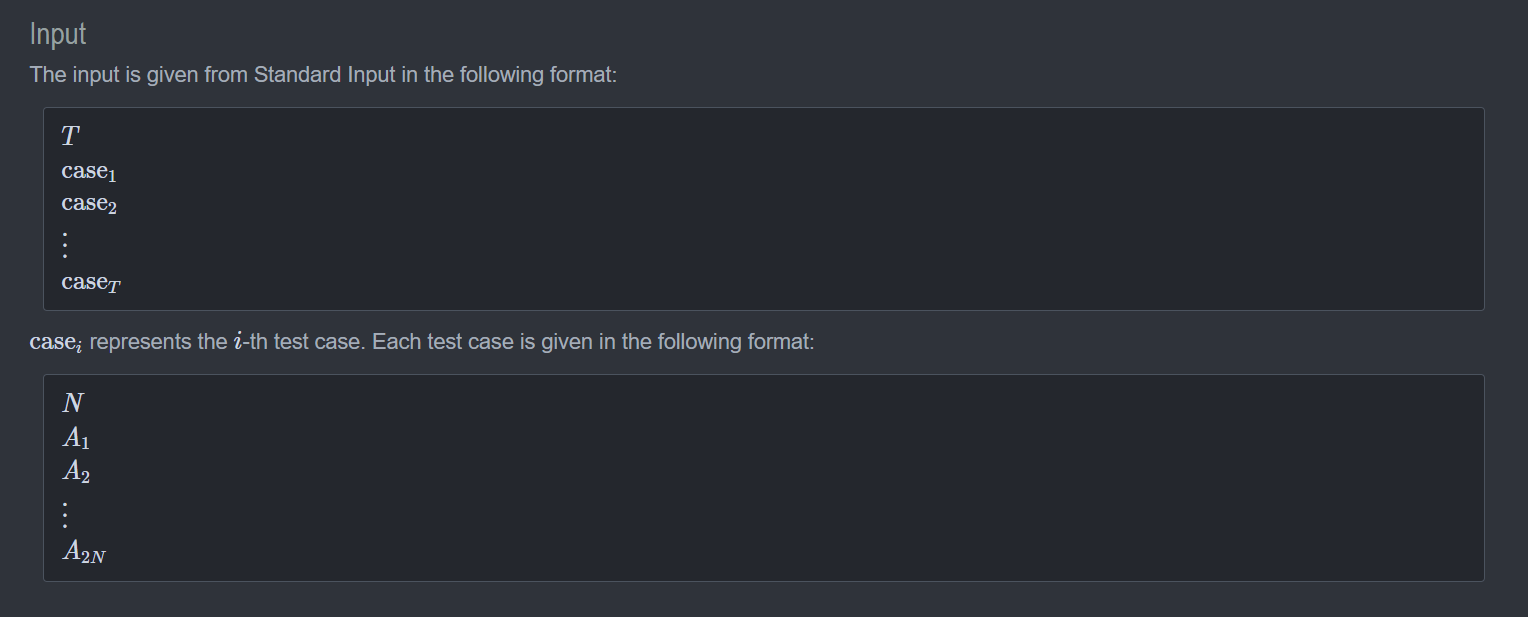
题解：

本题用到了括号序列的经典结论，即如果令左括号为1，右括号为-1，那么对于一个合法的括号序列，它的每个前缀值都大于等于0，且最终和为0。

那么对于本题有：对于i位置，需要满足右括号的个数不超过i//2，但是最终右括号的的个数应该是n//2。

因此这里维护最小的n//2个右括号的，遍历的过程中将遇到的元素放入最大堆(保证最终由n//2个右括号)，一旦堆的大小超过了i//2那么就弹出最大值(保证左括号和最大)。

for _ in range(R()):
    n=R()
    nums=[R() for _ in range(2*n)]
    h=[]
    for i in range(2*n):
        c=(i+1)//2
        heappush(h,-nums[i])
        while len(h)>c:
            heappop(h)
    print(sum(nums)+sum(h))